The Laws of Circuit - you can learn and practice by just reading

copyright. Charles Kim 2006

 

DELTA TO Y (D2Y) TRANSFORMATION

 

When two weapons of resistance simplification, i.e., series and parallel resistance, do not work, and thus all the circuit minimization efforts are exhausted, we rely on this WMD (weapon of mass diminution) called "Delta-to-Y Transformation (D2Y)." As the name implies, D2Y is to convert three resistors connected to three nodes and shaped as the Greek letter delta (D) into a circuit of Y or inverted Y shape.   The idea behind is to break the stronghold of triangle (which is very strong in mechanical structure, and now you see they are strong even in electrical structure) into an easily manageable Y shape. The "delta" shape, in many cases, does not look like a delta. Instead, they may look like a circle, a box, or any shape. But what common to the delta and the other variations is that: (1) there are three nodes (I mean essential nodes whose definition is the nodes that have more than 2 branches.) and (2) resistors are connected sequentially to form a delta. The converted Y (it would be easier to imagine to move an inverted Y inside the delta) circuit, where three resistors (with different value of course than those in the delta circuit) keeps the same three nodes that were in the delta circuit, and as you see in the letter Y, there is additional node generated which is the common meeting point of all three Y resistors.

 

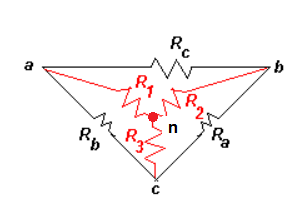
Now let's talk about the transformation rule or formula. I am not going to discuss how you prove the formula but I am going to tell you how you can easily memorize it. It is so easy you don't have to memorize it. I hate to bring up a figure, so in this discussion, I suggest you draw a circuit as I explained. Draw a delta shaped resistor circuit so that it resembles the Greek delta (D), pointy at top with bottom base. In your delta circuit, there are three nodes (label them a, b, and c) and three resistors connected into delta shape (label them Ra, Rb, and Rc). Then draw an inverted-Y shape resistor circuit inside the delta circuit with the same node locations. The central point node is labeled as "n". Label the three resistors R1, R2, and R3. The ordering in the resistors numbers like a, b, c, or 1, 2, 3 is not important at all. You can name them as you please.

 

Ok. This is the formula written in words. An Y-resistor (R1, R2, or R3) is the ratio of the multiplication of the two delta resistors that are positioned both side of the Y-resistor and the sum of all tree delta resistors. What I mean by the "delta resistors of both side of the Y-resistor" is that the two delta resistors connected to the same node with the Y-resistor in the middle. If you look at the Delta and Inverted Y circuits in the figure, all three nodes have three resistors connected: middle one is an Y resistor and the flanks (or two wings if you play soccer instead of football) are two delta resistors. So at a node, the middle one (R1 for example) is determined by the division of the multiplication of the two flanking delta resistors (Rb and Rc) by the sum of all three delta resistors (Ra+Rb+Rc). You apply this same rule at the other two nodes and you get the other two Y resistors. Simple isn't it. After you get all three Y resistors, you have to eliminate the delta resistors from your circuit. You cannot keep both the original and the converted. Keep only the Y resistors. Wipe the delta out.

 

When the "delta" shape is not apparent, placing Y or inverted Y is not apparent either. But remember, if you see three nodes with three resistors sequentially connected, they are delta shaped. I will tell you now how you place your Y or crooked Y or arrowed-shaped Y or whatever-shaped Y inside the whatever-shaped delta. It is not "placing" an Y. Instead in is forming an Y. Pick a node from the delta, and extend a short line from the node toward the general central position inside the delta and connect a resistor at the end of the sort line and extend a short line from the other end of the resistor toward the general central position inside the delta. Do this at the other two nodes. Now you see three resistors sprouted from the three nodes and they are about to meet around the center of the delta. Then you connect them into a node. You label the node "n." And the job is done with three resistors with Y shape formed with four nodes. Then apply the D2Y formula to find the values of the Y resistors. Delete and erase the delta resistors thanking them for their sacrifice. But you gotta eliminate them.

 

Warning 1: Do not abuse the D2Y. There are a lot of circuit crooks out there (I confess I am one of them) who makes a simple circuit look like a delta resistors and fools you and spoils your exams and tests. First, check if there are any series resistors can be simplified. Second, check if there are any parallel resistors that can be simplified. Third, check if there are any further candidates that can be eliminated by series or parallel simplification. If you are 100% sure that there is no more simplification by series or parallel alone, then you check there are three nodes and three resistors forming nice or ugly delta shape. Apply D2Y only when you get through all the steps. Remember D2Y is the last hidden card. If you place and use too early, you are out of the game early. D2Y must be the last resort.

 

Warning 2: When you see multiple delta resistors in a circuit, apply D2Y to just one delta and see how the transformation changes the whole circuit. If you are exhausted with series and parallel simplification, then find another delta for D2Y application. Do not apply D2Y to two delta circuits at the same time. Doing that is not wrong but it may increase the possibility that you use a delta resistor twice to D2Y, especially when the delta circuits are adjacent. You shall not use a delta resistors in two D2Y cases. Once a delta resistor is used in D2Y, that resistor must be trashed. It should not be recycled.

WWW.MWFTR.COM